카메라 왜곡 보정 - Spherical model

카메라 왜곡 보정 - Spherical model

2024. 8. 18. 15:55ㆍ카테고리 없음

카메라 왜곡을 보정하기 위해 사용하는 모델 중 하나로 스피리컬 모델(Spherical Model)이 있습니다. 이 모델은 주로 피쉬아이 렌즈(Fisheye Lens) 같은 넓은 화각을 가진 렌즈에서 발생하는 왜곡을 보정하는 데 사용됩니다. 스피리컬 모델을 이해하기 위해 기본적인 카메라 왜곡과 보정 방법을 먼저 설명한 후, 스피리컬 모델에 대해 자세히 다루겠습니다.

카메라 왜곡 (Camera Distortion)

카메라 왜곡은 렌즈가 이미지에 비정상적인 변형을 가하는 현상입니다. 대표적으로 라디얼 왜곡(Radial Distortion)과 탄젠셜 왜곡(Tangential Distortion)이 있습니다.

라디얼 왜곡: 이미지의 중심으로부터 거리가 멀어질수록 선들이 휘어지는 현상입니다.
- 배럴 왜곡(Barrel Distortion): 직선이 외향으로 휘어지는 왜곡.
- 핀쿠션 왜곡(Pincushion Distortion): 직선이 내향으로 휘어지는 왜곡.
탄젠셜 왜곡: 렌즈와 이미지 센서가 완전히 평행하지 않을 때 발생하며, 이미지가 약간 기울어져 보이는 현상입니다.

스피리컬 모델 (Spherical Model)

스피리컬 모델은 주로 피쉬아이 렌즈와 같은 초광각 렌즈에서 발생하는 극심한 라디얼 왜곡을 보정하는 데 사용됩니다. 스피리컬 모델은 평면이 아닌 구면(Sphere)을 기준으로 이미지를 재투영합니다. 이 방식은 특히 넓은 화각에서 발생하는 왜곡을 더 정확하게 보정할 수 있습니다.

기본 원리

평면 투영 (Planar Projection): 일반적인 카메라 모델은 3D 세계를 2D 이미지 평면으로 투영합니다.
스피리컬 투영 (Spherical Projection): 스피리컬 모델은 이미지를 구면 위에 투영한 후 이를 평면으로 다시 투영합니다. 이 과정에서 왜곡이 줄어들게 됩니다.

수학적 표현

스피리컬 모델은 3D 좌표 ((X, Y, Z))를 구면 좌표로 변환한 후 다시 평면 좌표로 변환하는 과정을 거칩니다. 이 과정에서 왜곡을 보정합니다

1. 3D 좌표를 구면 좌표로 변환:

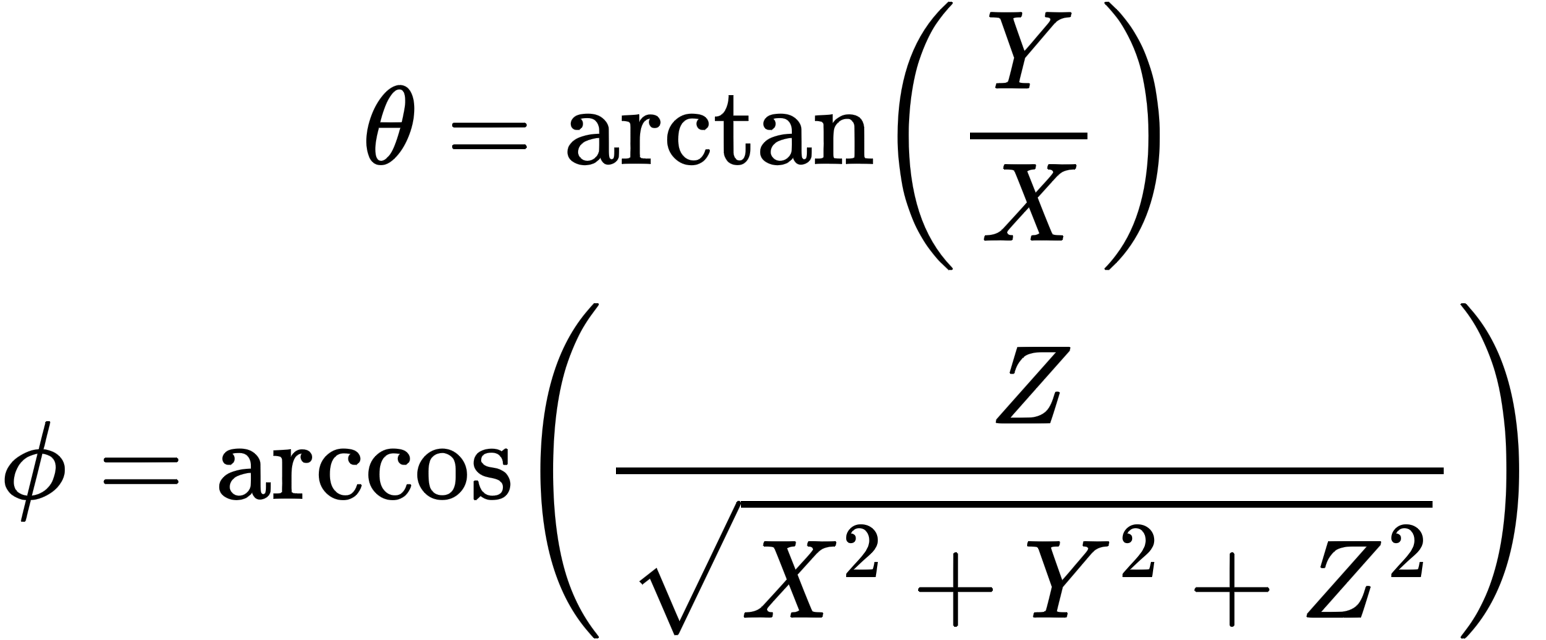
구면 좌표를 왜곡 보정된 평면 좌표로 변환:

Python 코드 예시

카메라 왜곡 보정을 위한 스피리컬 모델을 적용하는 기본적인 Python 코드입니다. OpenCV 라이브러리를 활용하여 구현할 수 있습니다.

import cv2
import numpy as np

def spherical_undistort(image, f):
    h, w = image.shape[:2]

    # 새로운 좌표를 담을 맵 생성
    map_x = np.zeros((h, w), dtype=np.float32)
    map_y = np.zeros((h, w), dtype=np.float32)

    # 중심 좌표
    cx = w / 2
    cy = h / 2

    for y in range(h):
        for x in range(w):
            # 좌표를 중심으로 이동
            x_shifted = (x - cx) / f
            y_shifted = (y - cy) / f

            # 구면 좌표로 변환
            r = np.sqrt(x_shifted**2 + y_shifted**2)
            theta = np.arctan(r)

            # 보정된 좌표 계산
            map_x[y, x] = cx + theta * x_shifted / r
            map_y[y, x] = cy + theta * y_shifted / r

    # 리매핑하여 보정된 이미지 생성
    undistorted_image = cv2.remap(image, map_x, map_y, interpolation=cv2.INTER_LINEAR)

    return undistorted_image

# 이미지 불러오기
image = cv2.imread('fisheye_image.jpg')

# 초점 거리 (f) 설정
f = 500  # 필요에 따라 조정

# 왜곡 보정
undistorted_image = spherical_undistort(image, f)

# 결과 저장
cv2.imwrite('undistorted_image.jpg', undistorted_image)

이 코드는 피쉬아이 렌즈로 찍은 이미지의 왜곡을 보정하는 스피리컬 모델을 적용한 예시입니다. f 값은 카메라의 초점 거리에 따라 조정해야 하며, 이를 통해 왜곡 정도를 조절할 수 있습니다.

Spherical model 활용 후 camera intrinsic parameter

스피리컬 모델을 사용하여 왜곡을 보정한 후의 이미지는 새로운 투영 방식을 가지기 때문에, 기존의 카메라 내재 파라미터(intrinsic parameters)와는 다르게 해석될 수 있습니다. 구체적으로 어떻게 변하는지 살펴보겠습니다.

기존 카메라 내재 파라미터 (Intrinsic Parameters)

기존의 카메라 모델에서는 카메라 매트릭스 K가 다음과 같은 형태로 주어집니다:

여기서:

fx, fy는 X와 Y 축에 대한 초점 거리(focal length).
cx, cy는 이미지 중심의 좌표(principal point).
이 매트릭스는 주로 직선 투영(Planar Projection)을 기반으로 하여 3D 점을 2D 이미지 평면으로 변환하는 데 사용됩니다.

스피리컬 모델에서의 변화

스피리컬 모델을 적용한 후에는 이미지가 구면 투영(Spherical Projection)을 기반으로 다시 재투영되므로, 기존의 카메라 내재 파라미터는 그대로 사용되지 않으며, 이미지의 기하학적 특성이 달라지게 됩니다. 특히 중요한 변화는 초점 거리와 이미지 중심의 해석 방법입니다.

초점 거리 (Focal Length):
- 기존 모델에서는 초점 거리 fx, fy가 X, Y 축 각각에 대해 정의되지만, 스피리컬 모델에서는 구면 좌표를 기준으로 재투영되기 때문에 이 값들은 변형됩니다.
- 스피리컬 모델의 초점 거리는 보정된 이미지의 크기와 관계가 깊으며, 이미지 중심에서의 반지름 값으로 해석될 수 있습니다.
이미지 중심 (Principal Point):
- 스피리컬 모델에서는 이미지 중심이 구면 투영에 따라 변형되므로, 기존의 중심 좌표 cx, cy도 다르게 해석됩니다. 이미지 중심은 스피어의 투영 중심으로 재설정됩니다.
왜곡 계수 (Distortion Coefficients):
- 스피리컬 모델에서는 전통적인 왜곡 계수(라디얼 및 탄젠셜 왜곡)가 더 이상 적용되지 않습니다. 따라서 이 값들은 스피리컬 모델의 결과 이미지에서는 의미가 없습니다.

새로운 내재 파라미터 정의

스피리컬 모델을 적용한 후의 새로운 내재 파라미터는 다음과 같이 재정의될 수 있습니다:

(f'): 스피리컬 투영 후의 효과적인 초점 거리. 이 값은 스피리컬 투영에 의해 결정되며, 이미지의 크기와 형태에 영향을 미칩니다.
(c_x'), (c_y'): 새로운 이미지 중심 좌표. 이 값들은 스피리컬 투영에 의해 결정된 새로운 중심 위치를 나타냅니다.

이러한 파라미터는 실제로 이미지의 구체적인 형태에 따라 달라지므로, 필요에 따라 다시 계산해야 합니다.

결론

스피리컬 모델을 사용하여 왜곡을 보정한 후에는 기존의 카메라 내재 파라미터가 그대로 적용되지 않으며, 새로운 투영 방식에 맞춰 다시 정의됩니다. 이 과정에서 초점 거리와 이미지 중심의 해석이 달라지며, 기존의 왜곡 계수는 더 이상 사용되지 않습니다. 따라서 스피리컬 모델로 변환된 이미지에 대해 새로운 내재 파라미터를 정의하거나 측정하는 과정이 필요합니다.

예시

스피리컬 모델을 적용한 후의 카메라 내재 파라미터(intrinsic parameters)를 계산하는 Python 코드를 작성할 수 있습니다. 이 코드에서는 보정된 이미지의 새로운 초점 거리와 중심 좌표를 계산합니다.

코드 설명

기존 카메라 매트릭스 K를 입력받습니다.
스피리컬 보정 후의 이미지 크기를 계산합니다.
새로운 초점 거리와 이미지 중심을 계산합니다.

import numpy as np

def calculate_new_intrinsics(K, f, original_shape, new_shape):
    """
    스피리컬 모델을 적용한 후 새로운 카메라 내재 파라미터를 계산합니다.

    :param K: 기존 카메라 내재 파라미터 (3x3 매트릭스)
    :param f: 스피리컬 투영에서 사용된 초점 거리
    :param original_shape: 기존 이미지의 크기 (h, w)
    :param new_shape: 보정된 이미지의 크기 (h', w')
    :return: 새로운 카메라 내재 파라미터 (3x3 매트릭스)
    """

    # 기존 카메라 매트릭스에서 초점 거리와 중심 좌표 추출
    f_x = K[0, 0]
    f_y = K[1, 1]
    c_x = K[0, 2]
    c_y = K[1, 2]

    # 원래 이미지 크기
    original_h, original_w = original_shape

    # 보정된 이미지 크기
    new_h, new_w = new_shape

    # 새로운 초점 거리 계산 (비율에 따라 조정)
    f_x_new = f * (new_w / original_w)
    f_y_new = f * (new_h / original_h)

    # 새로운 이미지 중심 계산
    c_x_new = new_w / 2
    c_y_new = new_h / 2

    # 새로운 카메라 매트릭스 구성
    K_new = np.array([
        [f_x_new, 0, c_x_new],
        [0, f_y_new, c_y_new],
        [0, 0, 1]
    ])

    return K_new

# 예제 입력값
K_original = np.array([
    [1000, 0, 640],
    [0, 1000, 360],
    [0, 0, 1]
])

f_spherical = 500  # 스피리컬 투영에서 사용된 초점 거리
original_shape = (720, 1280)  # 기존 이미지 크기 (height, width)
new_shape = (1024, 1024)  # 보정된 이미지 크기 (height, width)

# 새로운 내재 파라미터 계산
K_new = calculate_new_intrinsics(K_original, f_spherical, original_shape, new_shape)

print("새로운 카메라 내재 파라미터:")
print(K_new)

코드 동작 설명

초점 거리 조정: f_x_new와 f_y_new는 기존의 초점 거리 값에 스피리컬 모델에서 사용된 초점 거리 f를 곱하여, 새로운 이미지 크기에 맞게 조정됩니다.
이미지 중심 조정: c_x_new와 c_y_new는 보정된 이미지의 중심을 기준으로 다시 설정됩니다. 일반적으로 스피리컬 투영을 거친 후에는 이미지 중심이 이미지의 중앙에 위치하게 됩니다.
새로운 카메라 매트릭스 생성: 이 과정을 통해 생성된 새로운 카메라 매트릭스 K_new는 스피리컬 모델로 보정된 이미지에 대한 내재 파라미터를 나타냅니다.

이 코드를 통해, 기존 카메라 내재 파라미터를 기반으로 스피리컬 모델 적용 후의 새로운 내재 파라미터를 계산할 수 있습니다.

import numpy as np
import cv2

def fish2sphere(fisheye_img):
    # 입력 이미지 크기
    height, width = fisheye_img.shape[:2]
    
    # 구면 투영 이미지의 크기 설정 (2:1 비율)
    sphere_width = width
    sphere_height = width // 2

    # 구면 투영 이미지를 위한 빈 배열 생성
    sphere_img = np.zeros((sphere_height, sphere_width, 3), dtype=fisheye_img.dtype)

    # 어안 렌즈의 FOV 설정 (180도)
    FOV = np.pi  # 3.141592654

    for y in range(sphere_height):
        for x in range(sphere_width):
            # 구면 투영의 극좌표 계산
            theta = 2.0 * np.pi * (x / sphere_width - 0.5)  # -pi to pi
            phi = np.pi * (y / sphere_height - 0.5)  # -pi/2 to pi/2

            # 3D 공간의 벡터 계산
            psph_x = np.cos(phi) * np.sin(theta)
            psph_y = np.cos(phi) * np.cos(theta)
            psph_z = np.sin(phi)

            # 어안 렌즈의 각도 및 반경 계산
            theta_fish = np.arctan2(psph_z, psph_x)
            phi_fish = np.arctan2(np.sqrt(psph_x**2 + psph_z**2), psph_y)
            r_fish = width * phi_fish / FOV

            # 어안 렌즈 이미지에서의 픽셀 위치 계산
            pfish_x = 0.5 * width + r_fish * np.cos(theta_fish)
            pfish_y = 0.5 * width + r_fish * np.sin(theta_fish)

            # 어안 렌즈 이미지의 좌표가 유효한지 확인 후 색상 샘플링
            if 0 <= pfish_x < width and 0 <= pfish_y < height:
                sphere_img[y, x] = fisheye_img[int(pfish_y), int(pfish_x)]

    return sphere_img

# 이미지 로드
fisheye_img = cv2.imread('fisheye_image.jpg')

# 어안 렌즈 이미지를 구면 투영 이미지로 변환
sphere_img = fish2sphere(fisheye_img)

# 변환된 이미지 저장
cv2.imwrite('sphere_image.jpg', sphere_img)

# 이미지 보기
cv2.imshow('Spherical Image', sphere_img)
cv2.waitKey(0)
cv2.destroyAllWindows()

jaeha-lee